This post is hopefully the first in a series of examples and demos for the Generative Art node for the Sverchok addon for Blender.
This node is very strongly based on Structure Synth and can produce Lindermayer Systems (lsystems) and fractals as well as more random and interesting creations.
For some examples I've also given a link to an eisenscript version to be used in the original StructureSynth. These are not always exactly equivalent due to some differences between the two implementations but should help those who are more familiar with eisenscript make the transition to the xml format. I'm also most of the way through writing a program (using pyparsing) to translate from eisenscript to the xml format (eisenxml).
Sverchok is available on github. Download the zip version and install like any other Blender addon.
The documentation for the node is here.
I have also started a repo on github for Generative Art examples. These examples include the eisenxml and the json for the nodes (this can be imported into Sverchok using the Import button on the Sverchok panel). For some examples I've also included an eisenscript version.
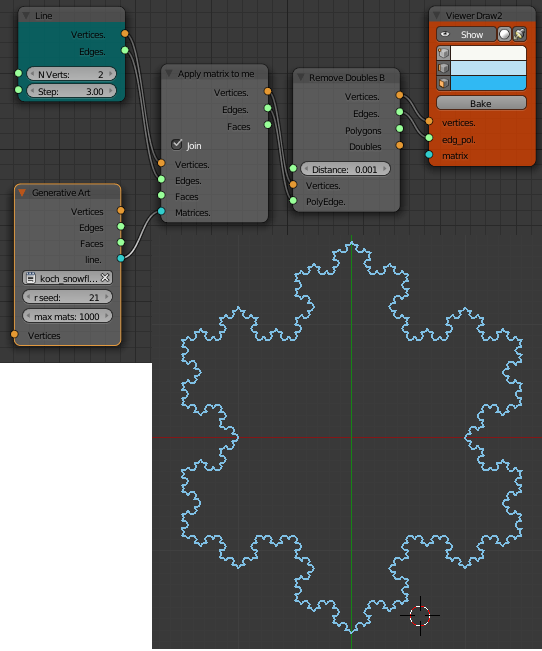
Koch Snowflake
<rules max_depth="100">
<rule name="entry">
<call transforms="ty 0.5*3**0.5" rule="R1"/>
<call transforms="rz 120 ty 0.5*3**0.5" rule="R1"/>
<call transforms="rz 240 ty 0.5*3**0.5" rule="R1"/>
</rule>
<rule name="R1" max_depth="4" successor="unit">
<call transforms="tx -1 sa 1.0/3.0" rule="R1"/>
<call transforms="tx -0.25 ty 0.25*3**0.5 rz 60 sa 1.0/3.0" rule="R1"/>
<call transforms="tx 0.25 ty 0.25*3**0.5 rz -60 sa 1.0/3.0" rule="R1"/>
<call transforms="tx 1 sa 1.0/3.0" rule="R1"/>
</rule>
<rule name="unit">
<instance transforms="tx -1.5 sa 1" shape="line"/>
</rule>
</rules>
This is one of the earliest fractals described (1904). The basic unit is only drawn at the smallest size. This is achieved by using the successor attribute in the R1 rule element. The successor attribute defines the rule to be called when the max_depth has been reached. That is after the R1 rule has been called recursively four times the unit rule is called.
xml, nodes in json, eisenscript, info
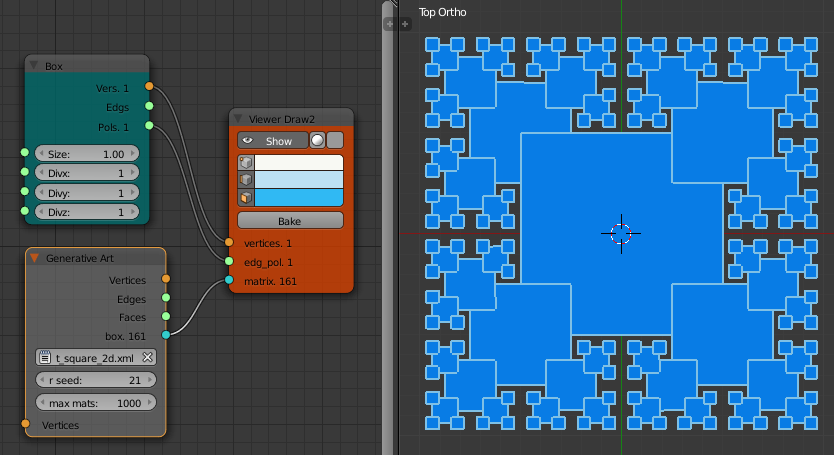
T-Square
<rules max_depth="100">
<rule name="entry">
<call rule="R1"/>
<call rule="R2"/>
</rule>
<rule name="R1" max_depth="5">
<instance transforms="sz 0.1" shape="box"/>
<call transforms="tx 0.5 ty 0.5 sx 0.5 sy 0.5 rz 90" rule="R1"/>
<call transforms="tx -0.5 ty -0.5 sx 0.5 sy 0.5 rz -90" rule="R1"/>
<call transforms="tx 0.5 ty -0.5 sx 0.5 sy 0.5" rule="R1"/>
</rule>
<rule name="R2" max_depth="4">
<call transforms="tx -0.5 ty 0.5 sx 0.5 sy 0.5 rz 180" rule="R1"/>
</rule>
</rules>
This fractal has the basic unit (a box) repeated at ever decreasing scales. at each iteration it is scaled in x and y by one half. The R1 rule places a box and then calls itself 3 times, rotating 90 degrees and scaling by a half each time. This places an ever decreasing set of boxes on three corners of the original box. Iterating over only three corners avoids placing boxes on the internal corner. The R2 rule finishes the fourth corner.
xml, nodes in json, eisenscript, info
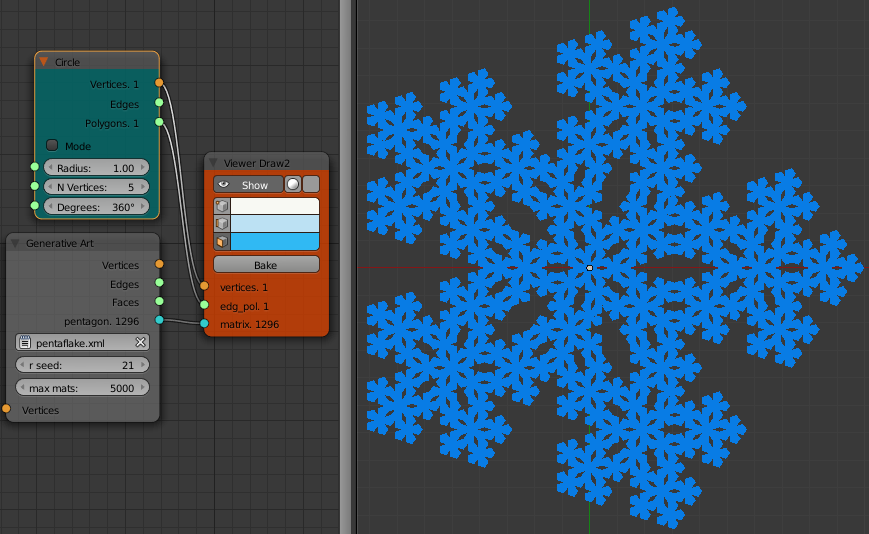
Pentaflake
<rules max_depth="100">
<rule name="entry">
<call rule="R1"/>
</rule>
<rule name="R1" max_depth="4" successor="pentagon">
<call transforms="rz 180 sa 0.382" rule="R1"/>
<call transforms="tx 0.618 sa 0.382" rule="R1"/>
<call transforms="tx 0.191 ty 0.5878 sa 0.382" rule="R1"/>
<call transforms="tx -0.5 ty 0.3633 sa 0.382" rule="R1"/>
<call transforms="tx -0.5 ty -0.3633 sa 0.382" rule="R1"/>
<call transforms="tx 0.191 ty -0.5878 sa 0.382" rule="R1"/>
</rule>
<rule name="pentagon">
<instance shape="pentagon"/>
</rule>
</rules>
The pentaflake is constructed by replacing a pentagon with six smaller pentagons. This in then repeated until the maximum depth is reached. this fractal is even older than the Koch curve appearing in a manuscript by Albrecht Durer in 1525. Its outer border is a version of the Koch snowflake. The structure is also closely related to the P1 Penrose tiling.

I've used approximate values for the scaling and transforms in the above xml. For the pedantic the values are given by:
Scaling:
\[\begin{align*} scale &= \frac{3-\sqrt{5}}{2} = 0.38197... \end{align*}\]Translation:
\[\begin{align*} t1 &= \frac{\sqrt{5} - 1}{2} = 0.61803...\\ t2 &= \frac{3-\sqrt{5}}{4} = 0.19098...\\ t3 &= \frac{1}{8}(\sqrt{10}-\sqrt{2})\sqrt{5 + \sqrt{5}} = 0.58775...\\ t4 &= \frac{1}{8}(\sqrt{10}-\sqrt{2})\sqrt{5 - \sqrt{5}} = 0.36325... \end{align*}\]See Larry Riddle's page for some of the derivations.
The xml processor used in the Generative Art node will evaluate math expressions in the transform definitions. For example the first call in the above xml could be written:
<call transforms="rz 180 sa (5**0.5-1)/2" rule="R1"/>
The python math and random modules have been imported into the node namespace so the call could also be written:
<call transforms="rz 180 sa (math.sqrt(5)-1)/2" rule="R1"/>
There cannot be any spaces in any maths expressions for the rotation, translation or scale parameters when using a single transforms attribute string (The spaces are used to split the string into its components). To allow for more complicated expressions each transform can be separated out into its own attribute. Notice the expression for sa (scale all) now has spaces in the expression.
<call rz="180" sa="(math.sqrt(5) - 1)/2" rule="R1"/>
The math expression string is passed to python's eval() function. The string must evaluate to a single number (float or integer). No checking is done for anything stupid or harmful in the string.
Constants can be defined and used in the xml like this:
<rules max_depth="100">
<constants scale="(3-5**0.5)/2" t1="(5**0.5-1)/2" t2="(3-5**0.5)/4" />
<constants t3="((10**0.5-2**0.5)*(5+5**0.5)**0.5)/8" t4="((10**0.5-2**0.5)*(5-5**0.5)**0.5)/8" />
<rule name="entry">
<call rule="R1"/>
</rule>
<rule name="R1" max_depth="4" successor="pentagon">
<call transforms="rz 180 sa {scale}" rule="R1"/>
<call transforms="tx {t1} sa {scale}" rule="R1"/>
<call transforms="tx {t2} ty {t3} sa {scale}" rule="R1"/>
<call transforms="tx -0.5 ty {t4} sa {scale}" rule="R1"/>
<call transforms="tx -0.5 ty -1*{t4} sa {scale}" rule="R1"/>
<call transforms="tx {t2} ty -1*{t3} sa {scale}" rule="R1"/>
</rule>
<rule name="pentagon">
<instance shape="pentagon"/>
</rule>
</rules>
The value of a constant is defined in a constants element using attributes (eg. scale="(3-5**0.5)/2"). These constants can then be used later when defining transforms where the attribute/constant name is enclosed in curly brackets (eg, sa {scale}). This is implemented in the node code using python's format string syntax for substitution. Any of the restrictions on format field_names also apply to constant names.
If a field_name such as {scale} is not defined in a constants element in the xml then a node input is created with this name. In the node diagram a Float or Integer or similar node can be wired to this input. This allows for the geometry to be animated or for fast experiments with different attribute values.
The max_depth attribute value of rule R1 has been replaced by the {md} variable in the following xml.
<rules max_depth="100">
<constants scale="(3-5**0.5)/2" t1="(5**0.5-1)/2" t2="(3-5**0.5)/4" />
<constants t3="((10**0.5-2**0.5)*(5+5**0.5)**0.5)/8" t4="((10**0.5-2**0.5)*(5-5**0.5)**0.5)/8" />
<rule name="entry">
<call rule="R1"/>
</rule>
<rule name="R1" max_depth="{md}" successor="pentagon">
<call transforms="rz 180 sa {scale}" rule="R1"/>
<call transforms="tx {t1} sa {scale}" rule="R1"/>
<call transforms="tx {t2} ty {t3} sa {scale}" rule="R1"/>
<call transforms="tx -0.5 ty {t4} sa {scale}" rule="R1"/>
<call transforms="tx -0.5 ty -1*{t4} sa {scale}" rule="R1"/>
<call transforms="tx {t2} ty -1*{t3} sa {scale}" rule="R1"/>
</rule>
<rule name="pentagon">
<instance shape="pentagon"/>
</rule>
</rules>
The Generative Art node that uses this xml then acquires an extra input md which can be wired to another node. If no input is connected the variable value will default to zero.
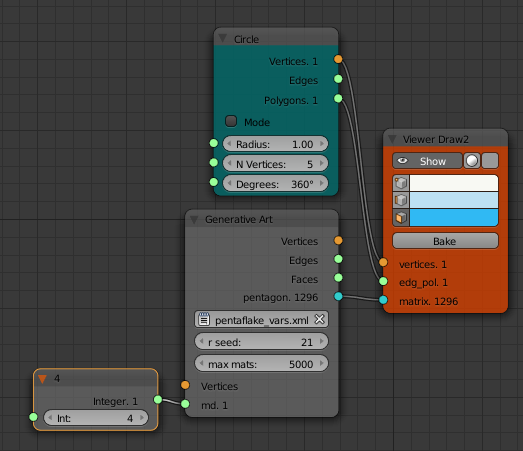
By varying the value of the Integer node it is very easy to produce a set of images to show each iteration of the pentaflake fractal.
