I was working with abstract sculptures in Blender based on polyhedra and was getting annoyed that the Regular Solids (part of the Extra Objects add-on) still divides polyhedron faces into quads and tris rather than using ngons for pentagonal faces for example. A quick look at the source code and it was obvious how to change this. But I started an Internet search on how the snub polyhedron were formed, this led to Conway Polyhedra and I was deep in a rabbit hole.
from Wikipedia
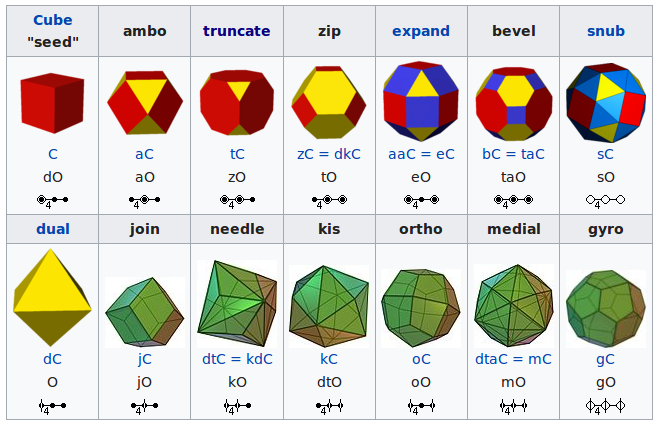
Conway Polyhedra are formed by applying various operators to a seed polyhedron such as one of the platonic solids. Some of the operators are similar to modifiers already present in Blender or nodes already in Sverchok. For example the ambo Conway operator is the same as the Bevel modifier with Only vertices checked and a Width of 1.0. The kis Conway operator is equivalent to Mesh > Faces > Poke Faces in edit mode.
Other of the Conway operators are more challenging to reproduce in Blender and Sverchok. I went searching expecting to find a python implementation of the Conway operators I could adapt to Sverchok but no luck. There is a very good online coffeescript app and Kit Wallace has a great openscad implementation
So I've written a module to implement a subset of the Conway operators in python. I've made the only dependency Blender's mathutils library. This means the code can be run outside Blender using a standalone version of the mathutils module.
Usage Notes
The conway.py module is designed to be used in Blender with Sverchok's Scripted Node Lite.
- Install Sverchok in Blender.
- Download and unzip (or clone) from the repo on github
- Open conway.py as a text block in Blender.
- Open snl_plato.py and snl_conway_op.py as text blocks in Blender. These contain code for each Sverchok Scripted Node Lite.
- In a Node Editor view create a new Node Tree and add two Scripted Node Lite nodes.
- Use the notebook icon on the node to select snl_plato.py on the left node and snl_comway_op.py on the right node. Click the plug icon on each node to load the code.
- Wire up the nodes along with a Viewer Draw node as shown below.
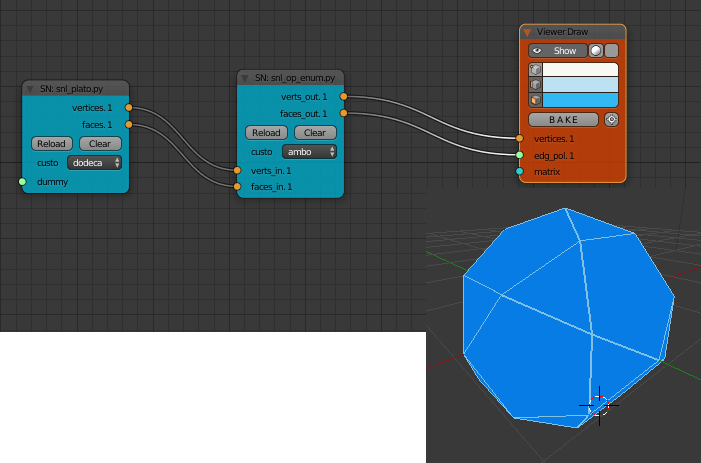
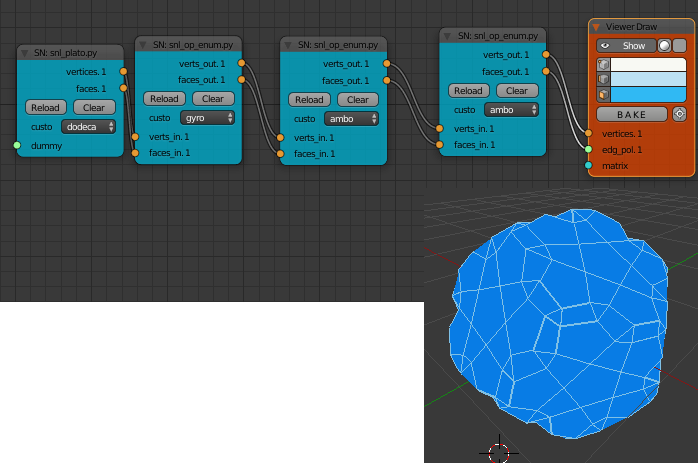
Wire up multiple copies of snl_conway_op.py in a row to produce more complex shapes.
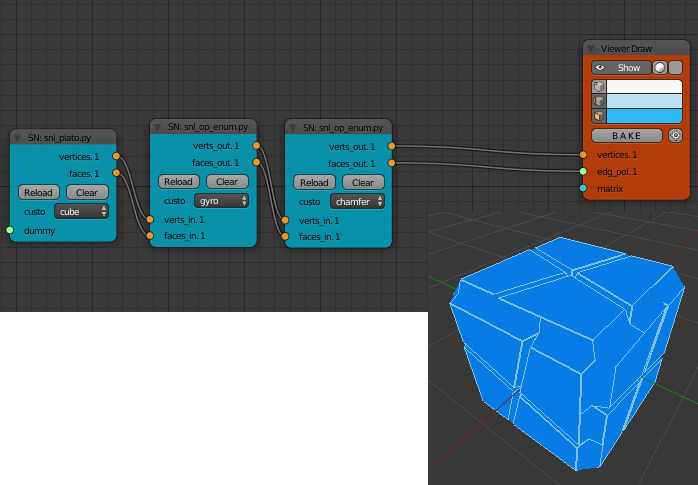
Two of the operators kis and chamfer can take parameters such as the height of the kis pyramid or the height and thickness of the chamfer. There is a separate Scripted Node Lite given for these two operators with sliders for the parameters.
Some operators, particularly gyro, propellor and whirl and chamfer give polyhedra that are not particularly smooth or convex, the faces may not be flat or symmetric.
The canonical form of a convex polyhedra has all faces planar and all edges tangential to the unit sphere. The centre of gravity of the tangential points is also at the centre of the same unit sphere.
The module canon.py contiains functions that attempt to shift the points of a polyhedron to satisfy these conditions. This is a iterative process and can take several hundred steps to converge.
To try this in Sverchok, add the canon.py and snl_canon.py files as text blocks in your Blender file and add snl_canon.py as a Scripted Node Lite. The node has two parameters iterations and scale_factor. At each iteration the vertices are moved a scale_factor fraction of the calculated distance. Setting this parameter too high may cause the shape to become unstable. Increasing the iterations will increase the calculation time.
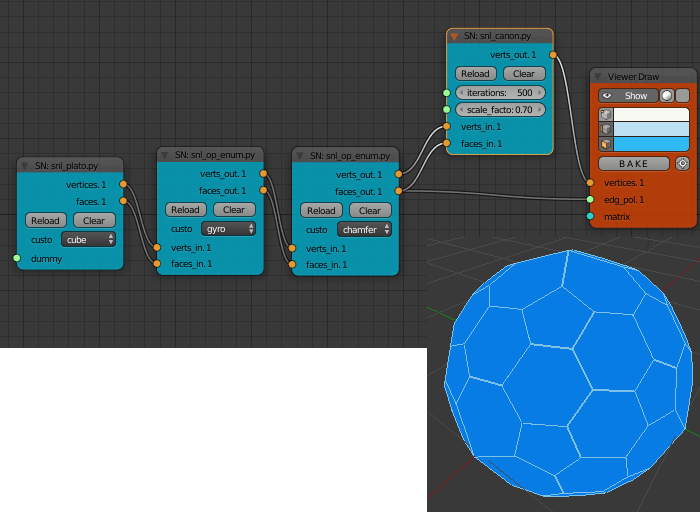
The canonicalization can also be applied after each operator. In the example below just enough iterations have been applied to form a pleasing shape. The proper canonical form of this polyhedra should be the same whether the canonicalization is performed once or twice.
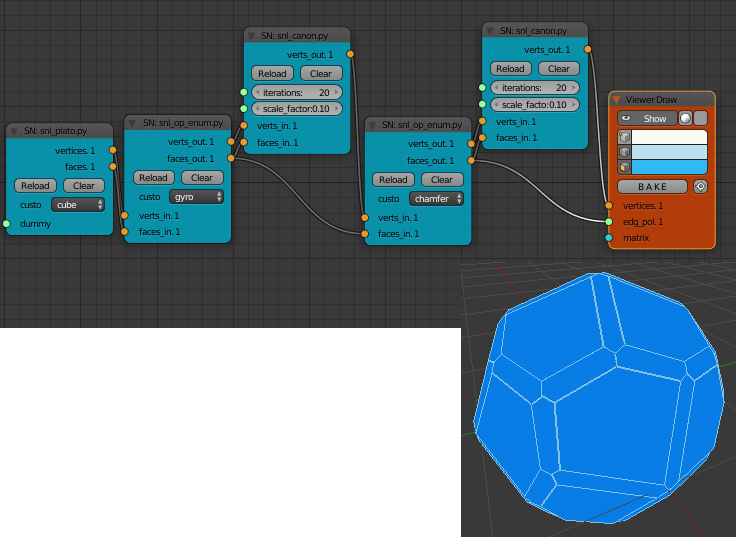
These Conway operators can be applied to any manifold (ie. a closed solid) mesh not just the platonic solids. They currently don't work on planar grids unless one applies a solidify node to the grid first.
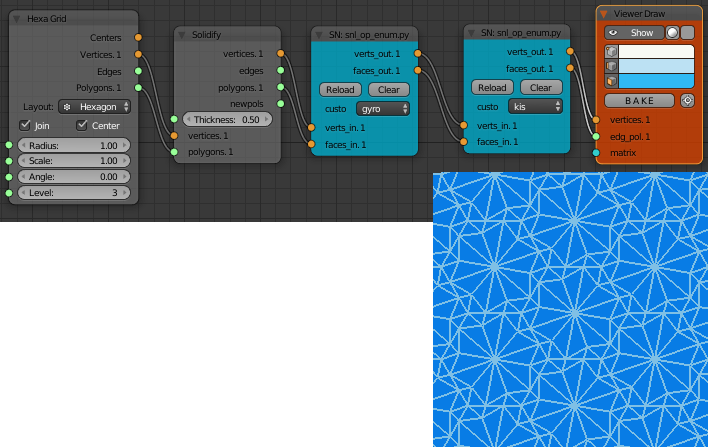
Other Sverchok nodes of course can be used interspersed with the Conway operators for other effects.
I've only implemented a subset of the operators defined on the Wikipedia page. Many of the operators are equivalent to a combination of other operators as shown in the chart
Conversion chart
The operator order is given as the left to right node order. Note that this is the opposite to the order given in the Conway notation.
| Operator | Description | Implementation |
|---|---|---|
| kis | poke face | node |
| dual | faces become vertices, vertices become faces | node |
| ambo | full vertex bevel | node |
| chamfer | hexagons replace edges | node |
| gyro | faces divided into pentagons | node |
| whirl | insets a smaller rotated copy of the face | node |
| propellor | insets a rotated copy of the face | node |
| zip | dual of kis | kis dual |
| expand | edge bevel | ambo ambo |
| bevel | vertex bevel applied twice | ambo dual kis dual |
| snub | dual of gyro | gyro dual |
| join | dual of ambo | ambo dual |
| needle | dual of truncate | dual kis |
| ortho | single subdivide | ambo ambo dual |
| meta | poke face and subdivide edges | ambo dual kis |
| truncate | half vertex bevel | dual kis dual |
Future
Ironically I haven't coded the snub operator directly, and I've used the code from add_mesh_extra_objects.add_mesh_solid to implement the platonic solids with n-gons.
Some of these operators would be useful as full nodes in Sverchok, particularly dual.
Make the operators work on open edge meshes.
Another way of making the polyhedra more "regular" would be to use an algorithm that evens up the edge lengths while leaving the vertices on the surface of the unit sphere. This could be done with a particle simulation similar to that I used for the Hyperbolic Plane generation. A much simpler approach would be to implement a simple version of a repulsion algorithm, iterating over each point and only calculating \(1/r^2\) repulsion forces for vertices connected by an edge.