This is part four of my introduction to Sverchok the parametric node geometry add-on for Blender. This post I'm sticking to my theme of copying one object to the structure (either the vertices or polygons) or another mesh. There is an awful lot more than just copying that can be done with Sverchok (see here for example) but copying is good for explaining the basics.
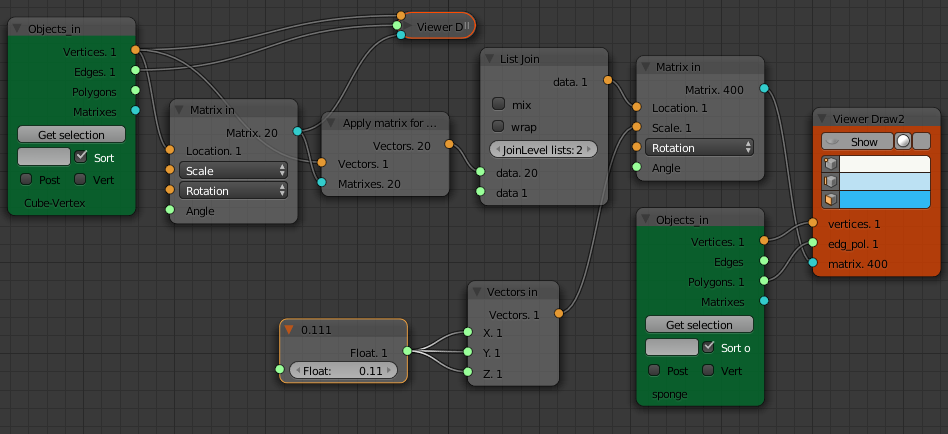
The very simple node tree below takes a copy of the cube, scales it to half size and places a copy on each each of the corners of the original large cube. The scale values are accessed by clicking on the scale drop down. We could also connect a "Vector In" node here to give the three scale values.
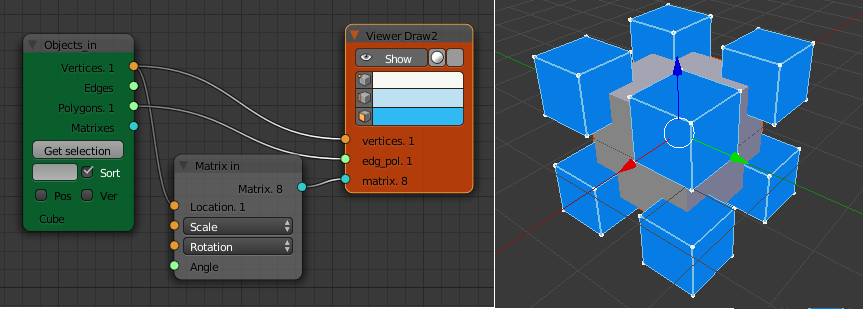
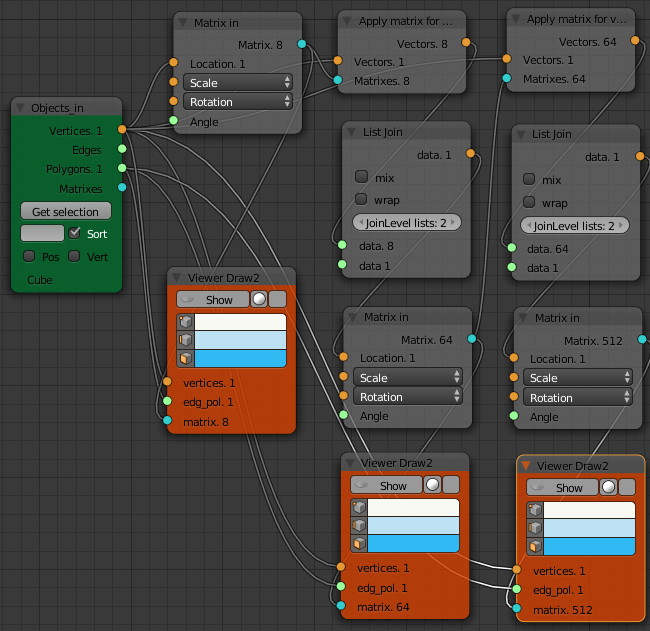
Very straight forward. How would we continue this copy in a recursive fashion to produce a fractal structure? That is copy a small cube (64 in total) to each corner of the eight mid-sized cubes. Then repeat this with 512 tiny cubes etc. This would produce a 3D version of the T-square fractal.
The "Viewer Draw" node takes a list of vertices from the "Object In" node and a list of matrices defining the location of each of vertices of the original cube and a scale factor to apply to each of the copies. To do another level of copying we need a list of matrices that give the location of the corners of the eight mid-sized cubes.
The "Matrix Apply" node takes a list of vertices and a list of matrices and produces a nested list of vertices for all the mid sized cubes. Take a look at the output of the "Matrix Apply" node with the "Viewer Text" node. It consists of a nested list with three levels. The outermost level (level 1) contains 8 objects, one for each cube. Each of these level 1 objects contains eight lists (level 2), one for each corner of a cube. Each of these level 2 list contains three numbers (level 3) for the x, y, z coordinates of the vertex.
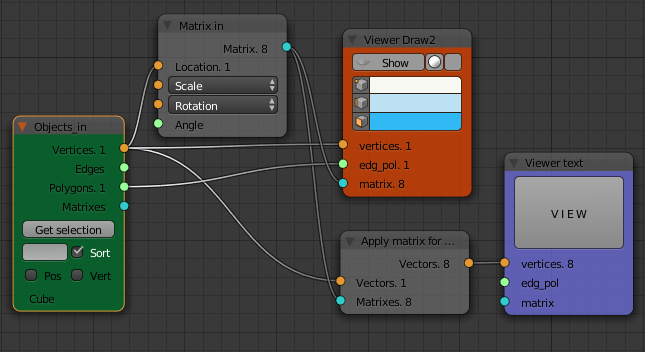
vertices:
(8) object(s)
=0= (8)
(1.5, 1.5, -1.5)
(1.5, 0.5, -1.5)
(0.5, 0.5, -1.5)
(0.5, 1.5, -1.5)
(1.5, 1.5, -0.5)
(1.5, 0.5, -0.5)
(0.5, 0.5, -0.5)
(0.5, 1.5, -0.5)
=1= (8)
(1.5, -0.5, -1.5)
(1.5, -1.5, -1.5)
(0.5, -1.5, -1.5)
(0.5, -0.5, -1.5)
(1.5, -0.5, -0.5)
(1.5, -1.5, -0.5)
(0.5, -1.5, -0.5)
(0.5, -0.5, -0.5)
....
We need to flatten this list so it contains 1 object with a list of 64 vertices. This is done using the "List Join" node with the "JoinLevelLists" set to 2. Check with the "Viewer Text" node that this is what happened.
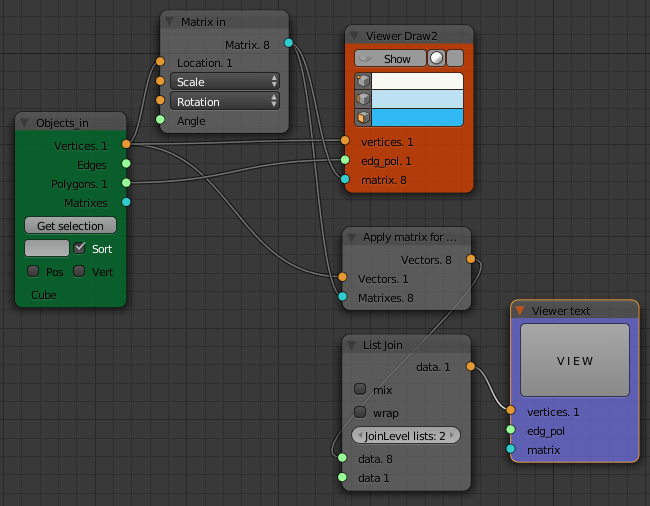
vertices:
(1) object(s)
=0= (64)
(1.5, 1.5, -1.5)
(1.5, 0.5, -1.5)
(0.5, 0.5, -1.5)
(0.5, 1.5, -1.5)
(1.5, 1.5, -0.5)
...
We then feed this list into another "Matrix In" node, set the scale values and send the resulting list of 64 matrices to another "Viewer Draw" node. We can repeat this process as many times as we like to get a fractal structure.

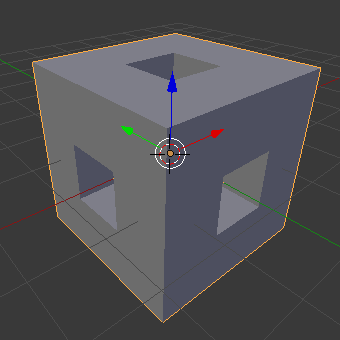
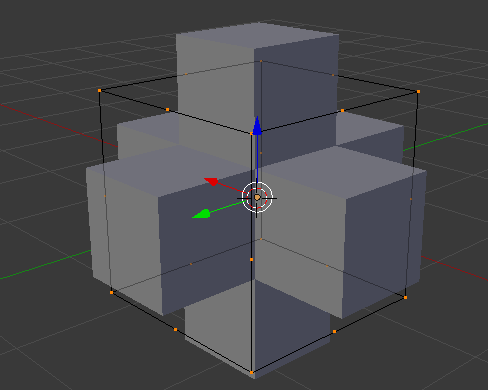
Another simple 3D fractal is the Menger Sponge. The sponge (right) and its negative space (left) are shown below. The sponge and its negative would fit together to completely fill a cube.

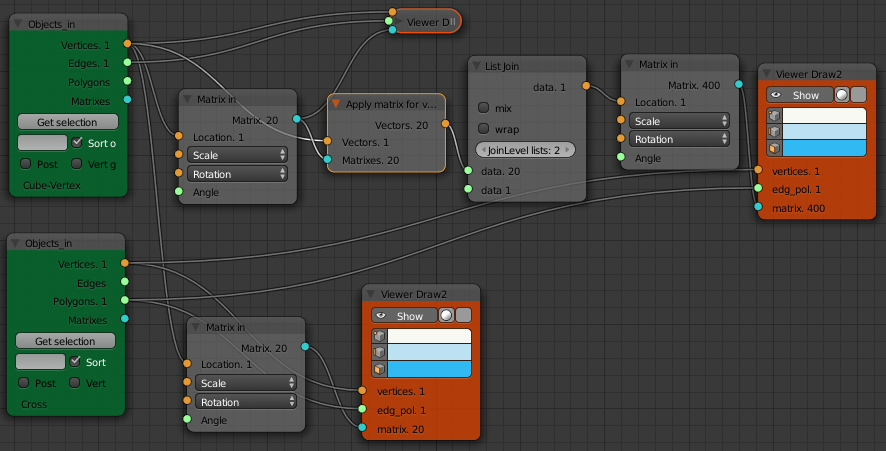
Looking at these, the negative sponge looks easier to build by copying. The basic underlying structure is shown below. The structure consists of ever smaller copies of the central cross. The cross can be made by extruding each face of a cube. The positions to copy to are given by the wire frame cube. This is made by deleting the faces from a cube and subdividing each edge. The cross should be three units across and the wire frame cube 2 units across.
For the first level of copying (the bottom row on the following node tree) we just copy the Cross to the Cube vertices of the wireframe. The second level of copying is done in the top row. The scale factors for each "Matrix In" node can be calculated or found by trial and error. They are for the two nodes in the top row (from left to right) 0.33 (1/3) and 0.1666 (1/6) and 0.5 (1/2) for the "Matrix In" node in the bottom row.

More levels of smaller copies can be made in a similar way.
Once we understand the use of a separate mesh to define the copy to points, constructing the positive Menger Sponge is just as simple. We start by making the base unit which is the boolean difference between a cube and our previous base cross object. The wire frame object is the same as for the negative sponge. Once having set up the recursive scaled copy of the wire frame mesh we only need to copy one size of unit sponge object to each vertex position. The scale factor is 1/9 for a a basic sponge unit of dimension 3 and three levels of recursion.